I learned this visualization of the chain rule from one of my grad school officemates. It draws on the fact that “and” usually goes with multiplication (more on that in its own post eventually).

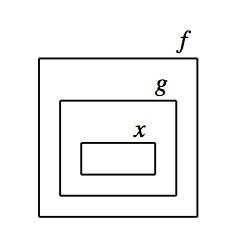
Imagine when you have f(g(x)) that x is a little sealed box. It is inside a second sealed box marked g, and that box is in a third sealed box marked f.

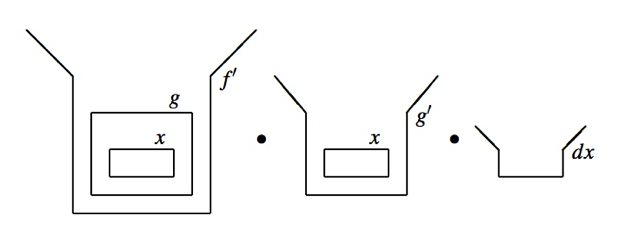
To differentiate you open the box marked f, and remove and open the box marked g, and remove and open the box marked x. The open boxes are the derivatives of the closed boxes, and containment still represents composition.

All put together, the drawing above represents the derivative of f(g(x)):